
x变化,导致y随之发生了变化
机器学习所关心的问题之一是捕捉函数的变化趋势,也就是研究y如何随着x而变,这个趋势是通过求导和微分来实现的。
连续性是函数的性质之一,它是可以对函数求导的前提条件。
具有连续性的函数,y值随x值的变化是连贯不间断的。并不是所有函数都具有连续性,像上面提到的阶跃函数从-1到1的跃迁明显就不具有连续性。
然而,有连续性的函数对于机器学习来说至关重要。因为机器学习的过程总体来说是对趋势和函数的变化规律的学习。失去了连续性,趋势和变化的规律也就难以用下面所要介绍的方法寻找了。
导数(derivative)是定义在连续函数的基础之上的。想要对函数求导,函数至少要有一段是连续的。导数的这个“导”字命名得好,导,是引导,是导航,它与函数上连续两个点之间的变化趋势,也就是与变化的方向相关。
看下面这张图,在一段连续函数的两个点A、B之间,y值是怎么从A点逐渐过渡到B点的?是因为x的变化,y也随之发生了变化,这个变化记作dx,dy。
为了演示得比较清楚,A、B两点离得比较远,通过一条割线,就可以把dx,dy割出来。这个割线给出的方向,就是从A点到B点的变化,也就是割线的斜率。初中数学讲过,直线的斜率就是它相对于横轴的倾斜程度,求法是dy/dx,也等价于从A点到B点的变化方向。

x变化,导致y随之发生了变化
那么当A点和B点的距离越来越小,两个点无限接近,逼近极限的时候,在即将重合而又未重合的一刹那,割线就变成切线了,如下图所示。
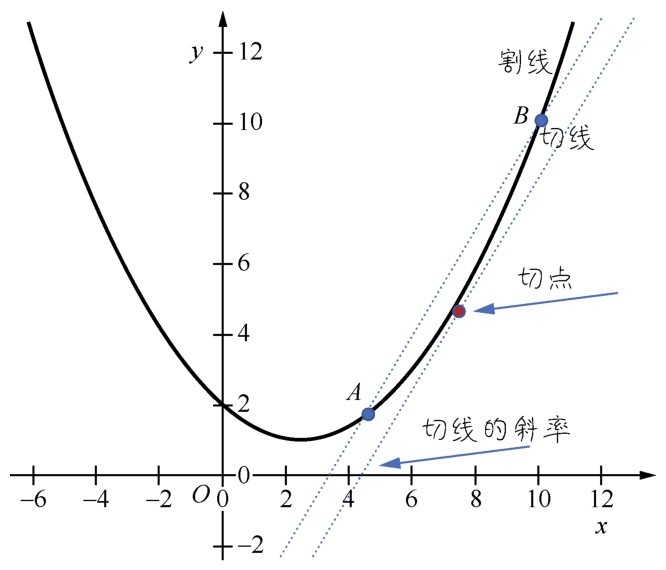
对切点求导所得的值,就是切线的斜率
而此时,对切点求导所得的值,就是切线的斜率。
■当斜率为正的时候,说明函数目前变化趋势是在上升。
■当斜率为负的时候,说明函数目前变化趋势是在下降。
■当斜率为0的时候,说明函数正处于全局或者局部的最低点,趋势即将发生改变。
总结一下:函数变化的趋势至少由两个点体现,即当A趋近于B的时候,求其变换的极限,这就是导数。导数的值和它附近的一小段连续函数有关。如果没有那么一段连续的函数,就无法计算其切线的斜率,函数在该点也就是不可导的。
通过求导,实现了以直代曲,也发现了y值随x值而变化的方向。引申到机器学习领域,通过导数就可以得到标签y随特征x而变化的方向。
导数是针对一个变量而言的函数变化趋向。而对于多元(即多变量)的函数,它关于其中一个变量的导数为偏导数,此时保持其他变量恒定。如果其中所有变量都允许变化,则称为全导数。
 咖哥发言
咖哥发言
我们经常听说n元n次方程式,或者n元n次函数,其中的“元”,指的是自变量x的个数;其中的“次”,指的是x的指数的最大值。
在微积分中,可微函数是指那些在定义域中所有点都存在导数的函数。
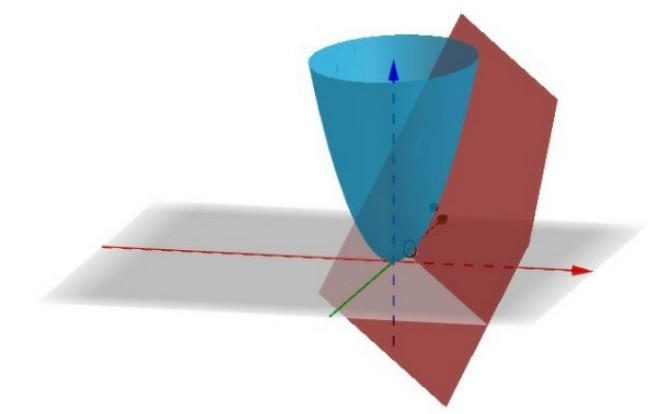
一个可微的二元函数
右图所示为一个可微的二元函数(对应机器学习中特征轴是二维的情况),这时候对函数求导,切线就变成了切面。
凹凸性也是函数的性质之一(函数还有很多其他性质,如奇偶性、单调性、周期性等),在这里只说说什么是凸函数。凸函数的定义比较抽象,这里只通过函数图形从直观上去理解。首先,函数形状必须是连续的,而不是断续的。其次,函数平滑,只存在一个最低点,整个函数呈现碗状。而非凸函数,可能呈现各种形状,有很多个底部(机器学习里面叫作局部最低点)。下图所示的函数f1就是一个凸函数,而函数f2就不是一个凸函数。
在连续函数图像上的局部或者全局最低点对函数求导,导数值都为0。
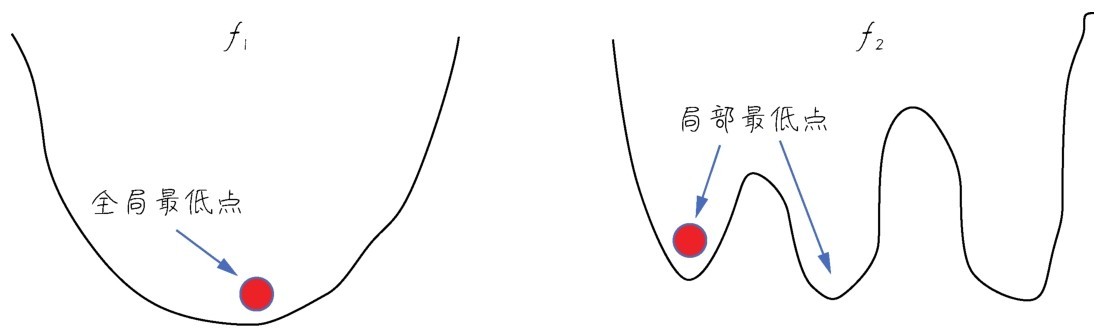
凸函数和非凸函数
为什么要特别讲这个凸函数呢?因为在机器学习的梯度下降过程中,只有凸函数能够确保下降到全局最低点。你们可能注意到我在上面的图像里面画了一个小球,凸函数的小球不管初始位置放在哪里,都可以沿着导数给出的方向滚到最低点;而在其他非凸函数中,小球就可能卡在半路,也就是那个叫作局部最低点的地方。在机器学习中,无法达到全局最低点是很不理想的情况(这是后话,暂且不讲解)。