表1-1 机器学习的基本术语

咖哥问:“刚才我们进行了一次简单的机器学习项目实战,并且介绍了几个Jupyter Notebook开发平台。现在考一考同学们已经学过的内容。谁能说说机器学习的定义是什么?”
一位同学回答:“机器学习,就是机器基于输入数据集中的信息来训练、确立模型,对以前从未见过的数据做出有用的预测。”
咖哥说:“总结得不错。下面给出机器学习中其他一些基本术语的定义,如表1-1所示。”
表1-1 机器学习的基本术语

再稍微详细地说一说上表中最为重要的3个术语:特征、标签和模型。
特征是机器学习中的输入,原始的特征描述了数据的属性。它是有维度的。特征的维度指的是特征的数目(不是数据集里面样本的个数),不同的数据集中的数据特征的维度不同,有多有少。
■少,可以少到仅有一个特征,也就是一维特征数据。比如房价(标签)仅依据房屋面积(特征)而定。
■多,可以多到几万,几十万。比如一个100px×100px的RGB彩色图片输入,每一个像素都可以视为一个特征,也就是1万维,再乘以RGB 3个颜色通道,那么这个小小的图片数据的特征维度就可以达到3万维。
举例来说,如果预测商品的销量,把商品的类别、价格和推荐级别这3个属性定义为商品的特征,那么这个数据集就是三维特征数据集。其中的一个样本的格式如下:
(x1,x2,x3)
然而,所谓三维特征,其实只是二维数据结构中的一个轴(另一个轴是样本轴)上的数据个数。为了避免混淆,我们以后会把向量、矩阵和其他张量的维度统称为阶,或者称为1D向量、2D矩阵、3D张量等。因此,以后一提“维”,主要指的就是数据集中特征X的数目。一般来说,特征维度越高,数据集越复杂。这里的“维”和“阶”有点绕,以后还会反复强调。
 咖哥发言
咖哥发言
这里提到的张量是机器学习的数据结构,其实也就是程序中的数组。在第2课中,才会很详细地讲解各种张量的结构。向量、矩阵都是张量的一种。简单地理解,向量张量是一个1D数组,而矩阵张量是一个2D数组。
标签,也就是机器学习要输出的结果,是我们试图预测的目标。示例里面的标签是房价。实际上,机器学习要解决什么问题,标签就是什么。比如:未来的股票价格、图片中的内容(猫、狗或长颈鹿)、文本翻译结果、音频的输出内容、Alpha Go的下一步走棋位置、自动导购汽车的行驶方向等。
下面是一个有标签数据样本的格式:
(x1,x2,x3;y)
标签有时候是随着样本一起来的,有时候是机器推断出来的,称作预测标签y'(也叫y-hat,因为那一撇也可放在y的上方,就像是戴了一个帽子的y)。比较y和y'的差异,也就是在评判机器学习模型的效果。
表1-2显示的是刚才实战案例中加州房价数据集中的部分特征和标签。
表1-2 加州房价数据集中的特征和标签
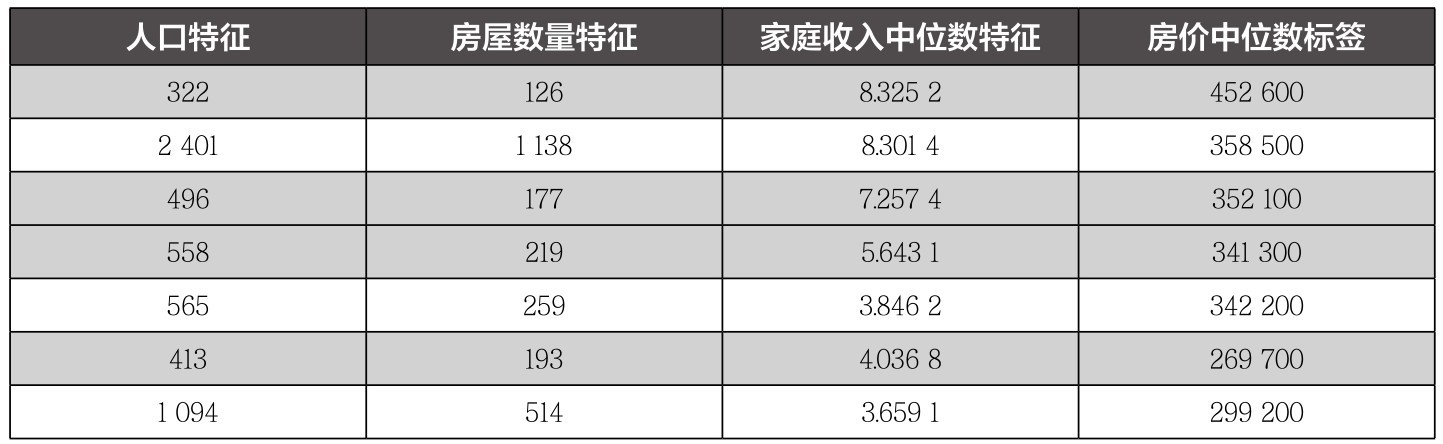
并不是所有的样本都有标签。在无监督学习中,所有的样本都没有标签。
模型将样本映射到预测标签y'。其实模型就是函数,是执行预测的工具。函数由模型的内部参数定义,而这些内部参数通过从数据中学习规律而得到。
在机器学习中,先确定模型的类型(也可以说是算法),比如是使用线性回归模型,还是逻辑回归模型,或者是神经网络模型;选定算法之后,再确定模型的参数,如果选择了线性回归模型,那么模型f(x) = 3x + 2中的3和2就是它的参数,而神经网络有神经网络的参数。类型和参数都确定了,机器学习的模型也就最终确定了。